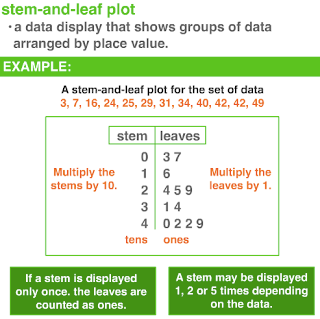
I found a link that has some helpful information about box and whisker plots. It goes through the steps of finding the different quartiles.
This link talks about Measures of Center.
Wednesday, May 2, 2012
Thursday, April 19, 2012
Wednesday, April 11, 2012
April 11, 2012
How is stats different than mathematics?
Stats concentrate on the context of the numbers. The analysis
Mathematics is how you get the numbers/data
Stats concentrate on the context of the numbers. The analysis
Mathematics is how you get the numbers/data
What questions would you ask if you were teaching a lesson on mean?
Mathematical Find the mean of the class spelling scores.
Statistical - What do these scores/mean tell me?
What is the difference between statistical questions and mathematical questions?
Mathematical questions are asking you to find an answer/number. Finding the statistic is a mathematical problem.
Statistical questions are asking to analyze those answers/number. Statistics is interpreting the data.
How to formulate an appropriate statistical question
- Consider what the data is
- where you are getting the data
- formulate a question that is free of bias
- Look at the research, make sure it is valid research
Key with Data Analysis - you don't do the analysis until you do the math. The math comes first, the analysis comes next.
Data Collection
- Tally marks
- tables
- pictographs
- bar graphs
- line graphs
- frequency tables
- line plots
- stem and leaf plot
- circle graphs
- histograms
- box and whisker plots
Wednesday, March 21, 2012
March 21. 2012
Danny's mother made cookies for his party. She made 36 cookies, The girls ate 1/4 of them. The boys ate 1/3 of them. If the 10 parents at the party shared the rest equally, how many cookies did each parent get?
With this Valentine's Day dance problem, the most important piece of information in this problem that can help you get the right answer is the fact there are only 3 rectangular table that will hold 8 people at each table.
My strategy for this problem was to move the names around as I read the problem the second time. Can you think of other strategies to solve this problem? Using manipulatives that represent the different teams, using a continuum line, write a list.
Strategy for this problem: guess and check. Figure out what the numbers could be for the rectangle and see if they would work for the square.
With this Valentine's Day dance problem, the most important piece of information in this problem that can help you get the right answer is the fact there are only 3 rectangular table that will hold 8 people at each table.
My strategy for this problem was to move the names around as I read the problem the second time. Can you think of other strategies to solve this problem? Using manipulatives that represent the different teams, using a continuum line, write a list.
How many other combinations of bracelets can Tiffany purchase without going over $20?
Strategy for this problem: put the smallest numbers in the corners.
Strategy for this problem: guess and check. Figure out what the numbers could be for the rectangle and see if they would work for the square.
Wednesday, March 14, 2012
March 15, 2012
Problem Solving Practices
(Best way to teach these? Post them where your students do their work and always point out what students are doing these practices)
- Get students to contextualize (put the numbers and put them in real world problems) and decontextualize (to remove from a context)
- Have students construct viable arguments and critique the reasoning of others
- Model with mathematics
- students can use concrete models, pictures, real-world situations, oral language and symbols
- Use appropriate tools strategically
- It's not always appropriate to use a calculator
- Attend to precision
- students are being precise in their math. Ex. using vocabulary correctly, labeling their units..
- Look for and make use of structure
- Look for and express regularity in repeated reasoning
What is the value of having students learn through problem solving?
- Problem solving is very engaging
Problem Solving Checklist
- Understand the question
- what are you being asked to do?
- What is important/not important
- Choose a plan
- What are you going to try to solve this problem?
- Try your plan
- Execute your plan
- Check your answer
- is it resonable, does it make sense?
- Reflect on what you've done
- whether or not your plan worked, reflect on what happened. Why did it or didn't it work? What when right or what went wrong?
What strategies could you use to solve the problem above?
- Draw pictures
- Guess and check
- Corey and Tommy are at a 6:2 ratio
- You could make a table
- You could write a system of equations (if you know how to do this)
 |
| Copy of a Parent Letter that you can send home. Tips on helping their student with problem solving. |
1. How many packets do we need? How many feet is the border?
Below is my solution
Problem Solving Strategy Icons
Problem solving Recording Sheet.
How to teach contextual clues and not just keywords
- Don't teach problem solving as a separate thing, it should be integrated
- Teach them how to identify key words that are commonly associated with mathematical operations.
- Teach students how to think aloud
- Teach students how to get to the bottom of the problem
- Teach students how to draw a picture
- Teach students how to create a table with the information provided
- Teach students how to identify the important/not important information/missing information
Wednesday, February 29, 2012
February 29 - Problem Solving
Problem Solving Strategies
Definition of a problem:
Definition of a problem:
- To truly be a problem, a mathematical quest must contain some effort of thought on the part of the solver.
As teachers, we must remember that what is a problem for some students may not be for others
Good problems include modifications that may be made for students with varying abilities.
Problem Solving Checklist
- Understand the question
- Choose a plan
- Try your answer
- Check your answer
- Reflect on what you've done
Corey, Chloe, and Tommy raised money for the Housing Project in the ration 6:3:2. Corey raised 3 dollars more than Tommy. How much money was raised all together?
Wednesday, February 15, 2012
The Pythagorean Theorem Rap (This video is just to help students remember the Pythagorean Theorem
Scientific Notation
*Note - BrainPop has an excellent video on scientific notation. It gives a great explanation.
Wednesday, February 8, 2012
February 8, 2012
Surface Area
Volume
Prisms
Cylinder
Cone
Volume
Prisms
Cylinder
Cone
Nets
Different Nets for Cubes
Finding the Surface Area
Finding the Volume
Area of the base x the height of the shape
Pyramids
Square Root
Subscribe to:
Comments (Atom)