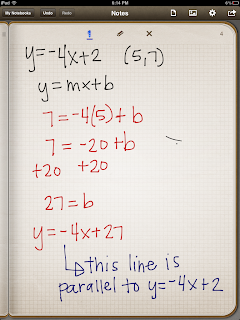Find a line that is perpendicular to another line
 |
| Remember: to find a perpendicular line the slope is the negative reciprocal to find a parallel line the slope stays the same always solve for b (the y intercept) |
Writing Linear Equations
- You must have the slope and the y=intercept in order to write a linear equation
- to find the slope use the formula m = y2-y1/x2-x1
- to find the y-intercept use the formula b = y - mx
Example:
Encourage teachers to think like their students as they discuss the attributes of the different shapes. What are rules you would use to sort these shapes?
 |
| #41 |
1. No straight edges vs straight edges
2. No vertices vs vertices
3. Line segments vs line segments
4. How many curves/curved sides
5. Parallel lines
6. Arcs
7. Concave vs convex
 |
| 1. Concave vs Convex 2. Vertices 3. # of Arcs 4. Angles vs no angles |
 |
| 1. # of sides 2. Angles 3. Concave vs. convex 4. Regular polygons vs irregular 5. # of peaks 6. Parallel vs nonparallel |
 |
| How would you sort these shapes? |
 |
| How would you sort these shapes? |
The total sum of the exterior angles of a triangle are 360 degrees
Sorting triangles
 |
| E = equilateral triangle H = equilateral triangle J = Right triangle, isosceles A = right, scalene F = Right, scalene I = right, scalene B = isosceles C = isosceles L = scalene G = isosceles |
Types of triangles :
- scalene - all three sides are different lengths
- isosceles - two sides of the triangle are the same length
- equilateral - all three sides are equal in length
- acute - all three angles are acute angles
- obtuse - triangle has an obtuse angle
- right - triangle has a right angle
**Technically in geometry you don't classify triangles as acute or obtuse**
Quadrilaterals
 |
| properties of sides:one pair of parallel sides, if non-parallel sides are equal the shape is an isosceles trapezoid properties of angles = can be 2 acute or 2 obtuse |
 |
| 2 sets of parallel lines 4 sides angels: opposite angles are the same properties of diagonals - nothing special here |
 |
| Properties of sides - all sides are parallel and equal in lengs Properties of angles: all right angles diagonals: perpendicular, bisect, and congruent |
 |
| properties of sides: all sides are equal in length properties of angles: opposite angles are equal, 2 obtuse and 2 acute diagonals: perpendicular and bisect |
 |
| Number of sides - 2 = how many triangles number of triangle x 180 = sum of interior angles |
The more sides of a polygon the smaller the exterior angles. All exterior angles add up to 360 degrees.
Homework
Read: Beckman 599-602